Learn Pytorch: Training your first deep learning models step by step

Here is my story: I recently gave a university tutoring class to MSc students on deep learning. Specifically, it was about training their first multi-layer perceptron (MLP) in Pytorch. I was literally stunned from their questions as beginners in the field. At the same time, I resonated with their struggles and reflected back to being a beginner myself. That’s what this blogpost is all about.

If you are used to numpy, tensorflow or if you want to deepen your understanding in deep learning, with a hands-on coding tutorial, hop in.

We will train our very first model called Multi-Layer Perceptron (MLP) in pytorch while explaining the design choices. Code is available on github.

Shall we begin?

Imports

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt

The torch.nn package contains all the required layers to train our neural network. The layers need to be instantiated first and then called using their instances. During initialization we specify all our trainable components. The weights typically live in a class that inherits the torch.nn.Module class. Alternatives include the torch.nn.Sequential or the torch.nn.ModuleList class, which also inherit the torch.nn.Module class. Layers classes typically start with a capital letter even if they don’t have any trainable parameters so feel like declaring them like:

The torch.nn.functional contains all the functions that can be called directly without prior initialization. Mosttorch.nn modules have their corresponding mapping in a functional module like:

A very handy example of a function I often use is the normalize function:

Device: GPU

Students despise using the GPU. They don’t see any reason to since they are only using tiny toy datasets. I advise them to think in terms of scaling up the models and the data, but I can see it’s not that obvious in the beginning. My solution was to assign them to train a resnet18 in 100K image dataset in google colab.

device = 'cuda:0' if torch.cuda.is_available() else 'cpu'
print('device:', device)

There is one and only one reason we use the GPU: speed. The same model can be trained much much faster in a high-end GPU.

Nonetheless, we want to have the option to switch to the CPU execution of our notebook/script, by declaring a “device” variable at the top.

Why? Well, for debugging!

It’s quite common to have GPU-related errors, which are actually simple logical errors, but because the code is executed on the GPU, pytorch is not able to trace back the error properly. Examples may include slicing errors, like assigning a tensor of wrong shape to a slice of another tensor.

The solution is to run the code on the CPU instead. You will probably get a more accurate error message.

GPU message example:

RuntimeError: CUDA error: device-side assert triggered

CUDA kernel errors might be asynchronously reported at some other API call,so the stacktrace below might be incorrect.

For debugging consider passing CUDA_LAUNCH_BLOCKING=1.

CPU message example:

Index 256 is out of bounds

Image transforms

We will use an image dataset called CIFAR10 so we will need to specify how the data will be fed in the network.

transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize(mean=(0.5, 0.5, 0.5), std=(0.5, 0.5, 0.5))])

Usually images are read from memory pillow images or as numpy arrays. We thus need to convert them to tensors. I won’t go into details into what pytorch tensors here. The important thing is to know that we can track gradients of a tensor and move them in the GPU. Numpy and pillow images don’t provide GPU support.

Input normalization brings the values around zero. One value for the means and std is provided for each channel. If you provide only one value for the mean or std, pytorch is smart enough to copy the value for all channels (transforms.Normalize(mean=0.5, std=0.5) ).

The images are in the range of $[0,1]$. After subtracting 0.5 and dividing by 0.5 the new range will be $[-1, 1]$.

Assuming that the weights are also initialized around zero, that is quite beneficial. In practice, it makes the training much easier to optimize. In deep learning we love to have our values around zero because the gradients are much more stable (predictable) in this range.

Why we need input normalization

If the images were in the $[0, 255]$ range that would disrupt the training much more severely. Why? Assuming that the weights initialized around 0, the output of the layer would be mostly dominated by large values, hence the large image intensities. That means that the weights will only be influenced by the large input values.

To convince you I wrote a small script for that:

x = torch.tensor([1., 1., 255.])
w = torch.tensor([0.1, 0.1, 0.1], requires_grad=True)
target = torch.tensor(10.0)
for i in range(100):
    with torch.no_grad():
        w.grad = torch.zeros(3)
    l = target - (x*w).sum()
    l.backward() 
    w = w - 0.01 * w.grad
print(f"Final weights {w.detach().numpy()}")

Which outputs:

Final weights [ 0.11    0.11    2.65]

In essence, only the weight that corresponds to the large input value changes.

The CIFAR10 image dataset class

trainset = torchvision.datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)
valset = torchvision.datasets.CIFAR10(root='./data', train=False, download=True, transform=transform)

Pytorch provides a couple of toy dataset for experimentation. Specifically, CIFAR10 has 50K training RGB images of size 32×32 and 10K test samples. By specifying the boolean train variable we get the train and test respectively. Data will be downloaded in the root path. The specified transforms will be applied while getting the data. For now we are just rescaling the image intensities to $[-1, 1]$.

The 3 data splits in machine learning

Typically we have 3 data splits: the train, validation and test set. The main difference between the validation and test set is that the test set will be seen only once. The validation performance metrics would be reliable to track the performance during training, even though the model’s parameters will not be directly optimized from the validation data. Still, we use the validation data to choose hyperparameters such as learning rate, batch size and weight decay (aka L2 regularization).

How to access this data?

Visualize images and understand label representations

def imshow(img, i, mean, std):
    unnormalize = transforms.Normalize((-mean / std), (1.0 / std))
    plt.subplot(1, 10 ,i+1)
    npimg = unnormalize(img).numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
img, label = trainset[0]
print(f"Images have a shape of {img.shape}")
print(f"There are {len(trainset.classes)} with labels: {trainset.classes}")
plt.figure(figsize = (40,20))
for i in range(10):
    imshow(trainset[i][0], i, mean=0.5, std=0.5)
print(f"Label {label} which corresponds to {trainset.classes[label]} will be converted to one-hot encoding by F.one_hot(torch.tensor(label),10)) as: ", F.one_hot(torch.tensor(label),10))

Here is the output:

Images have a shape of torch.Size([3, 32, 32])
There are 10 with labels: ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']

Example images from the Cifar10 dataset

Each image label will be assigned one class id:

id=0 → airplane
id=1 → automobile
id=2 → bird
. . .

The class indices will be converted to one-hot encodings. You can do this manually once to be 100% sure what it means by calling:

Label 6 which corresponds to frog will be converted to one-hot encoding by F.one_hot(torch.tensor(label),10)) as:  tensor([0, 0, 0, 0, 0, 0, 1, 0, 0, 0])

The Dataloader class

train_loader = torch.utils.data.DataLoader(trainset, batch_size=256, shuffle=True)
val_loader = torch.utils.data.DataLoader(valset, batch_size=256, shuffle=False)

The standard practice is to use only a batch of images instead of the whole dataset at each step. That’s why the dataloader class stacks together a lot of images with their corresponding labels in one batch at each step.

It is critical to know that the training data need to be randomly shuffled.

This way, the data indices are randomly shuffled at each epoch. Thus, each batch of images is representative of the data distribution of the whole dataset. Machine learning heavily relies on the i.i.d. assumption which means independent and identically distributed sampled data. This implies that the validation and test set should be sampled from the same distribution as the train set.

Let’s summarize the dataset/dataloader part:

print("List of label names are:", trainset.classes)
print("Total training images:", len(trainset))
img, label = trainset[0]
print(f"Example image with shape {img.shape}, label {label}, which is a {trainset.classes[label]} ")
print(f'The dataloader contains {len(train_loader)} batches of batch size {train_loader.batch_size} and {len(train_loader.dataset)} images')
imgs_batch , labels_batch = next(iter(train_loader))
print(f"A batch of images has shape {imgs_batch.shape}, labels {labels_batch.shape}")

The output of the above code is:

List of label names are: ['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
Total training images: 50000
Example image with shape torch.Size([3, 32, 32]), label 6, which is a frog 
The dataloader contains 196 batches of batch size 256 and 50000 images
A batch of images has shape torch.Size([256, 3, 32, 32]), labels torch.Size([256])

Building a variable size MLP

class MLP(nn.Module):
    def __init__(self, in_channels, num_classes, hidden_sizes=[64]):
        super(MLP, self).__init__()
        assert len(hidden_sizes) >= 1 , "specify at least one hidden layer"
        layers = nn.ModuleList()
        layer_sizes = [in_channels] + hidden_sizes
        for dim_in, dim_out in zip(layer_sizes[:-1], layer_sizes[1:]):
            layers.append(nn.Linear(dim_in, dim_out))
            layers.append(nn.ReLU())
        self.layers = nn.Sequential(*layers)
        self.out_layer = nn.Linear(hidden_sizes[-1], num_classes)
    def forward(self, x):
        out = x.view(x.shape[0], -1)
        out = self.layers(out)
        out = self.out_layer(out)
        return out

Since we inherit the torch.nn.Module class, we need to define the init and forward function. init has all the layers appended in the nn.ModuleList(). Module list is just an empty list that is aware that all the elements of the list are modules of the torch.nn package. Then we put all the elements of the list to torch.nn.Sequential. The asterisk (*) indicates that the layers will be passed as each layer being one input of the function like:

torch.nn.Sequential( nn.Linear(1,2), nn.ReLU(), nn.Linear(2,5), ...  )

When there are no skip connections within a block of layers and there is only one input and one output, we can just pass everything in the torch.nn.Sequential class. As a result, we will not have to repeatedly specify that the output of the previous layer is the input to the next one.

During forward we will just call it once:

y = self.layers(x) 

That makes the code much more compact and easy to read. Even if the model includes alternative forward paths formed by skip connections, the sequential part can be nicely packed like this.

Writing the validation loop

def validate(model, val_loader, device):
    model.eval()
    criterion = nn.CrossEntropyLoss()
    correct = 0
    loss_step = []
    with torch.no_grad():
        for inp_data, labels in val_loader:
            labels = labels.view(labels.shape[0]).to(device)
            inp_data = inp_data.to(device)
            outputs = model(inp_data)
            val_loss = criterion(outputs, labels)
            predicted = torch.argmax(outputs, dim=1)
            correct += (predicted == labels).sum()
            loss_step.append(val_loss.item())
        val_acc = (100 * correct / len(val_loader.dataset)).cpu().numpy()
        val_loss_epoch = torch.tensor(loss_step).mean().numpy()
        return val_acc , val_loss_epoch

Assuming we have a classification task, our loss will be categorical cross entropy. If you want to dive into why we use this loss function take a look at maximum likelihood estimation.

During the validation/test time, we need to make sure of 2 things. First, no gradients should be tracked, since we are not updating the parameters at this stage. Second, the model behaves as it would behave during test time. Dropout is a great example: during training we zero $p$ percent of the activations, while at test time it behaves like an identity function ($y =x$

• with torch.no_grad(): can be used to make sure we are not tracking gradients.

• model.eval() automatically changes the behavior of our layers to the test behavior. We need to call model.train() to undo its effect.

Next we need to move the data to the GPU. We keep using the variable device to be able to switch between GPU and CPU execution.

• outputs = model(inputs) calls the forward function and computes the unnormalized output prediction. People usually refer to the unnormalized predictions of the model as logits. Be sure you don’t get lost in the jargon jungle.

The logits will be normalized with softmax and the loss is computed. During the same call (criterion(outputs, labels)) the target labels are converted to one hot encodings.

Here is a thing that many students get confused on: how to compute the accuracy of the model. We have only seen how to compute the cross entropy loss. Well, the answer is rather simple: take the argmax of the logits.This gives us the prediction. Then, we compare how many of the predictions are equal to the targets.

The model will learn to assign higher probabilities to the target class. But in order to compute the accuracy we need to see how many of the maximum probabilities are the correct ones. For that one can use predicted = torch.max(outputs, dim=1)[1] or predicted = torch.argmax(outputs, dim=1). torch.max() returns a tuple of the max values and indices and we are only interested in the latter.

Another interesting thing is the value.item() call. This method can only be used for scalar values like the loss functions. For tensors we usually do something like t.detach().cpu().numpy(). Detach makes sure no gradients are tracked. Then we move it back to the cpu and convert it to a numpy array.

Finally notice the difference between len(val_loader) and len(val_loader.dataset). len(val_loader) returns the total number of batches the dataset was split into. len(val_loader.dataset) is the number of data samples.

Writing the training loop

def train_one_epoch(model, optimizer, train_loader, device):
    model.train()
    criterion = nn.CrossEntropyLoss()
    loss_step = []
    correct, total = 0, 0
    for (inp_data, labels) in train_loader:
        labels = labels.view(labels.shape[0]).to(device)
        inp_data = inp_data.to(device)
        outputs = model(inp_data)
        loss = criterion(outputs, labels)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        with torch.no_grad():
            _, predicted = torch.max(outputs, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum()
            loss_step.append(loss.item())
    loss_curr_epoch = np.mean(loss_step)
    train_acc = (100 * correct / total).cpu()
    return loss_curr_epoch, train_acc
def train(model, optimizer, num_epochs, train_loader, val_loader, device):
    best_val_loss = 1000
    best_val_acc = 0
    model = model.to(device)
    dict_log = {"train_acc_epoch":[], "val_acc_epoch":[], "loss_epoch":[], "val_loss":[]}
    pbar = tqdm(range(num_epochs))
    for epoch in pbar:
        loss_curr_epoch, train_acc = train_one_epoch(model, optimizer, train_loader, device)
        val_acc, val_loss = validation(model, val_loader, device)
        msg = (f'Ep {epoch}/{num_epochs}: Accuracy: Train:{train_acc:.2f} Val:{val_acc:.2f} \
                || Loss: Train {loss_curr_epoch:.3f} Val {val_loss:.3f}')
        pbar.set_description(msg)
        dict_log["train_acc_epoch"].append(train_acc)
        dict_log["val_acc_epoch"].append(val_acc)
        dict_log["loss_epoch"].append(loss_curr_epoch)
        dict_log["val_loss"].append(val_loss)
    return dict_log

• model.train() switches back the layers (e.g. dropout, batch norm) to their training behaviour.

The main difference is that backpropagation and the update rule come into play here through:

loss = criterion(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()

First, loss must always be a scalar. Second, each trainable parameter has an attribute called grad. This attribute is a tensor of the same shape of the tensor where gradients are stored. By calling optimizer.zero_grad() we go through all the parameters and replace the gradient values of the tensor to zero. In pseudocode:

for param in parameters:
    param.grad = 0

Why? Because the new gradients need to be computed during loss.backward(). During a backward call the gradients are computed and added to the previously-existing values.

for param, new_grad in zip(parameters, new_gradients):
    param.grad = param.grad + new_grad

That gives a lot of flexibility with respect to how often we could update our model. This would be beneficial for instance to train with a bigger batch size than our hardware enables us to, a technique called gradient accumulation.

In many cases we need to update the parameters at each step. Thus, the gradients need to be saved while deleting the values from the previous batch.

Computing the gradients is not updating the parameters. We need to go once again through all the model’s parameters and apply the update rule with optimizer.step() like:

for param in parameters:
    param = param - lr * param.grad

The rest is the same as in the validation function. Both losses and accuracies per epoch are saved in a dictionary for plotting later on.

Putting it all together

in_channels = 3 * 32 * 32
num_classes = 10
hidden_sizes = [128]
epochs = 50
lr = 1e-3
momentum = 0.9
wd = 1e-4
device = "cuda"
model = MLP(in_channels, num_classes, hidden_sizes).to(device)
optimizer = optim.SGD(model.parameters(), lr=lr, momentum=momentum, weight_decay=wd)
dict_log = train(model, optimizer, epochs, train_loader, val_loader, device)

Best validation accuracy: 53.52% on CIFAR10 using a two layer MLP.

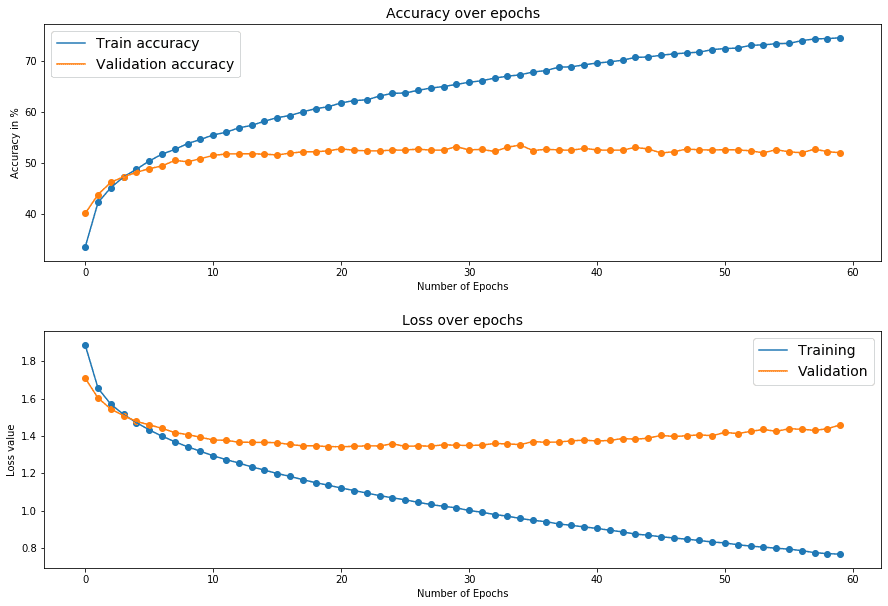
Losses and accuracies during training.

Design choices

So how do you design and train an MLP neural network?

• Batch size: very small batch sizes, typically < 8, may lead to unstable training or even fail, because of numerical issues. The default in a PyTorch Dataloader is 1, so make sure to always specify the batch size! Once a student was complaining that training takes 3 hours (instead of 5 minutes) because he forgot to specify the batch size. Use multiples of 32 for maximum GPU usage, if possible.

• Independent and Identically Distributed (IID): batches should ideally follow the IID assumption, so be sure to always shuffle your training data, unless you have a very specific reason not to.

• Always go from simple to complex design choices when designing models. In terms of model architecture and size this translates to starting from a small network. Go big if you think that performance saturates. Why? Because a small model may already perform sufficiently well for your use-case. In the meantime, you save tons of time, since smaller models can be training faster. Image that in a real-life scenario you will need to train your model multiple times to decide the best setup. Or even retrain it as more data becomes available.

• Always shuffle your training data. Don’t shuffle the validation and test set.

• Design flexible model implementations. Even though we start small and use only a hidden layer, there is nothing stopping us from going big. Our model implementation supports us having as many layers as we want. In practice, I have rarely seen an MLP with more than 3 layers and more than 4096 dimensions.

• Increase model dimensions in multiples of 32. The optimization space is insanely huge and makes wise choices like taking account of the hardware (GPU).

• Add regularization after you identify overfitting and not before.

• If you have no idea about the model size, start by overfitting a small subset of data without augmentations (check torch.utils.data.Subset).

To convince you even more, here is an online tutorial that someone used 3 hidden layers in CIFAR10 and achieved the same validation accuracy as us (~53%).

Conclusion & where to go next

Is our classifier good enough?

Well, yes! Compared to a random guess (1/10) we are able to get the correct class more than 50%.

Is our classifier good compared to a human?

No, human-level image recognition in this dataset would easily be more than 90%.

What is our classifier lacking?

You will find out in the next tutorial.

Please note the entire code is available on github. Stay tuned!

At this point you need to implement your own models into new datasets. An example: try to improve your classifier even more by adding regularization to prevent overfitting. Post your results on social media and tag us along.

Finally, if you feel like you need a structured project to get your hands dirty consider these extra resources:

Or you can try our very own course: Introduction to Deep Learning & Neural Networks

Deep Learning in Production Book 📖

Learn how to build, train, deploy, scale and maintain deep learning models. Understand ML infrastructure and MLOps using hands-on examples.

Learn more

* Disclosure: Please note that some of the links above might be affiliate links, and at no additional cost to you, we will earn a commission if you decide to make a purchase after clicking through.