Multi-agent path finding in continuous environments

Imagine if all of our cars could drive themselves – autonomous driving is becoming possible, but to what extent? To get a vehicle somewhere by itself may not seem so tricky if the route is clear and well defined, but what if there are more cars, each trying to get to a different place? And what if we add pedestrians, animals and other unaccounted for elements? This problem has recently been increasingly studied, and already used in scenarios such as warehouse logistics, where a group of robots move boxes in a warehouse, each with its own goal, but all moving while making sure not to collide and making their routes – paths – as short as possible. But how to formalize such a problem? The answer is MAPF – multi-agent path finding [Silver, 2005].

Multi-agent path finding describes a problem where we have a group of agents – robots, vehicles or even people – who are each trying to get from their starting positions to their goal positions all at once without ever colliding (being in the same position at the same time).

Typically, this problem has been solved on graphs. Graphs are structures that are able to simplify an environment using its focal points and interconnections between them. These points are called vertices and can represent, for example, coordinates. They are connected by edges, which connect neighbouring vertices and represent distances between them.

If however we are trying to solve a real-life scenario, we strive to get as close to simulating reality as possible. Therefore, discrete representation (using a finite number of vertices) may not suffice. But how to search an environment that is continuous, that is, one where there is basically an infinite amount of vertices connected by edges of infinitely small sizes?

This is where something called sampling-based algorithms comes into play. Algorithms such as RRT* [Karaman and Frazzoli, 2011], which we used in our work, randomly select (sample) coordinates in our coordinate space and use them as vertices. The more points that are sampled, the more accurate the representation of the environment is. These vertices are connected to that of their nearest neighbours which minimizes the length of the path from the starting point to the newly sampled point. The path is a sequence of vertices, measured as a sum of the lengths of edges between them.

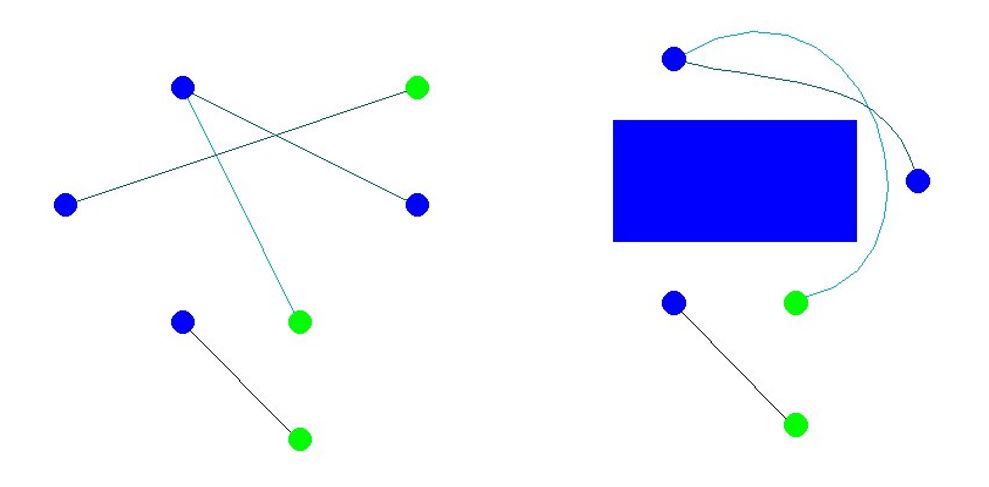Figure 1: Two examples of paths connecting starting positions (blue) and goal positions (green) of three agents. Once an obstacle is present, agents plan smooth curved paths around it, successfully avoiding both the obstacle and each other.

We can get a close to optimal path this way, though there is still one problem. Paths created this way are still somewhat bumpy, as the transition between different segments of a path is sharp. If a vehicle was to take this path, it would probably have to turn itself at once when it reaches the end of a segment, as some robotic vacuum cleaners do when moving around. This slows the vehicle or a robot down significantly. A way we can solve this is to take these paths and smooth them, so that the transitions are no longer sharp, but smooth curves. This way, robots or vehicles moving on them can smoothly travel without ever stopping or slowing down significantly when in need of a turn.

Our paper [Janovská and Surynek, 2024] proposed a method for multi-agent path finding in continuous environments, where agents move on sets of smooth paths without colliding. Our algorithm is inspired by the Conflict Based Search (CBS) [Sharon et al., 2014]. Our extension into a continuous space called Continuous-Environment Conflict-Based Search (CE-CBS) works on two levels:

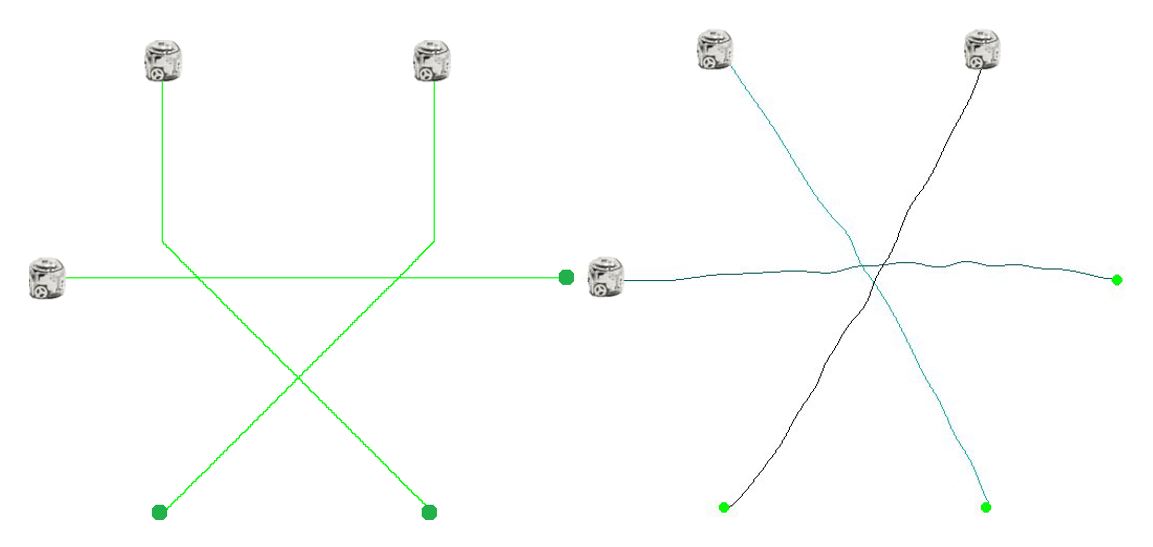Figure 2: Comparison of paths found with discrete CBS algorithm on a 2D grid (left) and CE-CBS paths in a continuous version of the same environment. Three agents move from blue starting points to green goal points. These experiments are performed in the Robotic Agents Laboratory at Faculty of Information Technology of the Czech Technical University in Prague.

Firstly, each agent searches for a path individually. This is done with the RRT* algorithm as mentioned above. The resulting path is then smoothed using B-spline curves, polynomial piecewise curves applied to vertices of the path. This removes sharp turns and makes the path easier to traverse for a physical agent.

Individual paths are then sent to the higher level of the algorithm, in which paths are compared and conflicts are found. Conflict arises if two agents (which are represented as rigid circular bodies) overlap at any given time. If so, constraints are created to forbid one of the agents from passing through the conflicting space at a time interval during which it was previously present in that space. Both options which constrain one of the agents are tried – a tree of possible constraint settings and their solutions is constructed and expanded upon with each conflict found. When a new constraint is added, this information passes to all agents it concerns and their paths are re-planned so that they avoid the constrained time and space. Then the paths are checked again for validity, and this repeats until a conflict-free solution, which aims to be as short as possible is found.

This way, agents can effectively move without losing speed while turning and without colliding with each other. Although there are environments such as narrow hallways where slowing down or even stopping may be necessary for agents to safely pass, CE-CBS finds solutions in most environments.

This research is supported by the Czech Science Foundation, 22-31346S.

You can read our paper here.

References

• Janovská, K. and Surynek, P. (2024). Multi-agent Path Finding in Continuous Environment, CoRR.
• Sharon, G., Stern, R., Felner, A., and Sturtevant, N. R. (2014). Conflict-based search for optimal multi-agent pathfinding, Artificial Intelligence.
• Karaman, S. and Frazzoli, E. (2011). Sampling-based algorithms for optimal motion planning, CoRR.
• Piegl, L. and Tiller, W. (1996). The NURBS Book, Springer-Verlag, New York, USA, second edition.
• Silver, D. (2005). Cooperative pathfinding, Proceedings of the First Artificial Intelligence and Interactive Digital Entertainment Conference, Marina del Rey, California, USA.